This post is the first in a series of example evaluations of interesting (to me) vector problems. There is plenty of literature available on the how and why of vector analysis. So while this series will not be a deep exploration, hopefully some of the problems and solutions are of interest for the reader.
Problem 1:
Given 3 vectors:
$$ \bar{a} = 3\bar{i} + 3\bar{j} + 3\bar{k} $$
$$ \bar{b} = -2\bar{i} + 3\bar{j} + \bar{k} $$
$$ \bar{a} = \bar{i} + 2\bar{j} + \bar{k} $$
Where i, j, and k represent unit vectors that form the basis for 3-dimensional Cartesian coordinates.
Determine the angle between a and b.
To determine the angle between two vectors, we can take advantage of the fact that in this case:
$$\bar{a} \cdot \bar{b} = \left | \bar{a} \right |\left | \bar{b} \right |cos(\theta ) = a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}
$$
Where:
$$ \left |\bar{a} \right | = \sqrt{3^{2}+6^{2}+9^{2}} $$
$$\left |\bar{b} \right | = \sqrt{(-2)^{2}+3^{2}+1^{2}}$$
$$\theta = arccos(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\left |\bar{a} \right | \left |\bar{b} \right | })$$
Given the above vectors, the above computation returns an angle of 60 degrees.
Problem 2:
Determine the constant angle between the radius vector and a tangent vector of the curve:
$$x(t) = e^{at}cos(t)$$
$$y(t)=e^{at}sin(t)$$
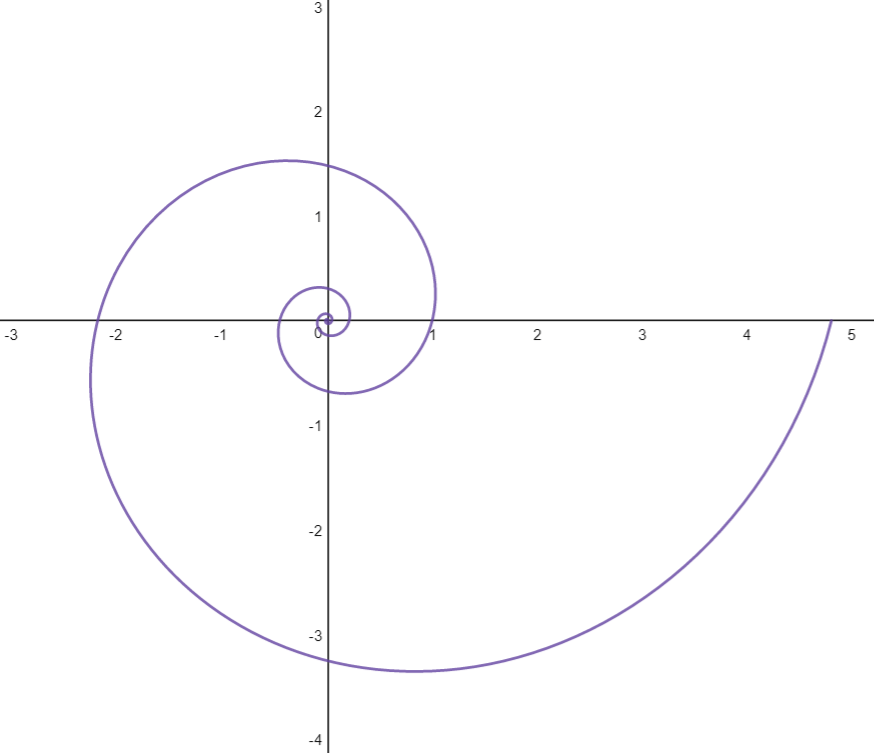
The above curve is referred to as a logarithmic spiral. This problem will be easier to solve in polar coordinates, where the basis for our coordinate system consists of a normalized basis vector pointing in the same direction as the radius vector, and a normalized basis vector pointing in the direction of increasing angle. These basis vectors are perpendicular. To solve this problem, I will need to define a radial coordinate as well as an angular coordinate.
Polar coordinates are related to the above x and y functions by the following equations:
$$x(t) = r(t)cos(\theta)$$
$$y(t) = r(t)cos(\theta)$$
$$r(t) = \sqrt{{x(t)}^2+{y(t)}^2}$$
In this case:
$$r(t) = e^{at} , \theta(t) = t $$
Position definition in polar coordinates requires the above r(t) to be multiplied by the unit vector in the direction of the radius vector. How do we get this unit vector?
We know that it needs to point in the direction of increasing r. We can find such a vector by differentiating the radius vector with respect to r. Similarly we could find the unit vector in the direction of increasing theta by differentiating with respect to theta.
$$\bar{r}(t) = x\bar{i}+y\bar{j} = rcos(\theta)\bar{i}+rsin(\theta)\bar{j} $$
$$\frac{\partial{\bar{r}}}{\partial{r}} = cos(\theta)\bar{i} + sin(\theta)\bar{j}$$
$$\frac{\partial{\bar{r}}}{\partial{\theta}} = -rsin(\theta)\bar{i} + rcos(\theta)\bar{j}$$
The above partials are in directions of increasing r and theta respectively. They are, however not unit vectors unless their magnitude is 1. Lets check the magnitude of each partial derivative:
$$h_{r} = \left \| \frac{\partial{\bar{r}}}{\partial{r}} \right \| = \sqrt{cos^2(\theta)+sin^2(\theta)} =1$$
$$h_{\theta} = \left \| \frac{\partial{\bar{r}}}{\partial{\theta}} \right \| = \sqrt{r^2sin^2(\theta)+r^2cos^2(\theta)} = \sqrt{r^2(1)} = r$$
We can use these magnitudes to normalize our partial derivatives to get unit vectors.
$$\hat{e}_{r}(\theta) = \frac{1}{h_{r}}\left \| \frac{\partial{\bar{r}}}{\partial{r}} \right \| = cos(\theta)\bar{i} + sin(\theta)\bar{j}$$
$$\hat{e}_{\theta}(\theta) = \frac{1}{h_{\theta}}\left \| \frac{\partial{\bar{r}}}{\partial{\theta}} \right \| = -sin(\theta)\bar{i} + cos(\theta)\bar{j}$$
We can see that the unit vectors are dependent on theta, which makes sense, as theta changes the perpendicular unit vectors will rotate about the origin.
Interestingly, taking the derivative of each with respect to theta we get the following result:
$$\frac{\partial{\hat{e}_{r}}}{\partial{\theta}} = -sin(\theta)\bar{i}+cos(\theta)\bar{j} = \hat{e}_{\theta}$$
$$\frac{\partial{\hat{e}_{\theta}}}{\partial{\theta}} = -cos(\theta)\bar{i}-sin(\theta)\bar{j} = -\hat{e}_{r}$$
So, we can define the radius vector with the following equation:
$$\bar{r} = r(t)\hat{e}_{r}(\theta(t))$$
Now we need to differentiate this position vector, because we are looking for the angle between this vector and the tangent vector which in this problem we will define as phi.
$$\frac{d\bar{r}}{dt} = \dot{r}(t)\hat{e}_{r}(\theta(t)) + r(t)\hat{e}_{\theta}\dot{\theta}(t)$$
This is the tangent vector. To find the angle between the two vectors (radius and tangent), we can take advantage of the following equations:
$$\frac{d\bar{r}}{dt} \cdot \bar{r} = \left | \frac{d\bar{r}}{dt} \right |\left | \bar{r} \right |cos(\phi)$$
$$\frac{d\bar{r}}{dt} \cdot \bar{r} = (\frac{d\bar{r}}{dt}\bar{r})\hat{e}_{r}+(\frac{d\bar{r}}{dt}\bar{r})\hat{e}_{\theta}$$
Recall that for this problem:
$$r(t) = e^{at} , \theta(t) = t $$
Solving the above two equations to find phi:
$$\frac{d\bar{r}}{dt} \cdot \bar{r} = e^{at}ae^{at} + (0)e^{at}(1)= \mathbf{a({e^{at}})^2}$$
$$\left | \bar{r} \right | = \mathbf{e^{at}}$$
$$\left |\frac{d\bar{r}}{dt} \right | = \sqrt{(ae^{at})^2+(e^{at})^2} = \mathbf{e^{at}\sqrt{a^2+1}}$$
$$cos{\phi} = \frac{ae^{at}}{e^{2at}\sqrt{(a^2+1)}} = \frac{a}{\sqrt{a^2+1}}$$
$$\phi = arccos(\frac{a}{\sqrt{a^2+1}})$$
We can see from the above equation that phi is only related to the value a, which impacts the rate of increase of the radius as t increases. Hence, it is the same across all t.
That took me a while… I will add an arc length calculation problem to this post if inspiration strikes at a later date.