The fastest anyone has ever gone on their own power on land is 89 miles per hour and change, in a vehicle called the Aerovelo Eta.

The first thing I noticed is the lack of apparent windscreen. If you’re also curious about that, the vehicle pilot sees with a display connected to a camera sticking out of the fairing body. This is a remarkable vehicle, here’s a look at the inside:

I was curious: how big is this achievement? What does it take to go this fast? Could someone achieve 100 miles per hour? I will break down what it might take to go this fast in a vehicle like the Aerovelo Eta.
Power
It takes power to go fast here on Earth. So lets see what it might take to reach 100 mph under human power.
On a bicycle like Eta you have to accelerate a mass (you and the bike) to 100 mph, while friction of the tires on the road, and air on the vehicle both hold you back. I’ll ignore acceleration and say that the power required to go fast comes from overcoming rolling resistance and aerodynamic drag. Also note that all of the power must be transferred from the person through the drive-train of the vehicle. This makes power equal to rolling resistance plus aerodynamic drag all over drive-train efficiency.
$$P_{total} = \frac{P_{R}+P_{D}}{\eta}$$
Rolling Resistance
The equation governing power to overcome rolling resistance:
$$P_{R}=vmg*C_{rr}$$
Where \(P_{R}\) is power to overcome rolling resistance. \(v\) is velocity in meters per second. \(m\) is mass in kilograms. \(g\) is acceleration due to gravity in meters per second squared. \(C_{rr}\) is the coefficient of rolling resistance.
Solving for mass, I will assume weights of a 175 lb person on a 50 lb vehicle. This makes \(m\cong100 kg\)
Solving for coefficient of rolling resistance is trickier without testing. Interestingly tests for a variety of tires can be found here. Wikipedia links this plot, for some experimental test data of a few tires at different speeds:

I’ll take the Schwalbe One tires, and extrapolate the \(C_{rr}\) roughly out to 100mph (~45m/s). This gives \(C_{rr}=.008\) Now we can solve for \(P_{R}\).
$$P_{R}=(45)(100)(9.81)*.008\cong 345$$
345 watts is the amount of power it takes to overcome rolling resistance at 100mph on a bicycle. This shows how important it is to select tires that have a low rolling resistance. For instance, Continental Grand Prix 5000 TL tires have a \(C_{rr}\) of .00249 at 8m/s, significantly lower than the tires in the plot. Extrapolating that tire out along similar curves as the others, one might achieve .0015 lower \(C_{rr}\). Which results in:
$$P_{R}=(45)(100)(9.81)*.0065\cong 281$$
281 watts is 64 watts saved. Tire selection matters at 100 mph. For this analysis, I will use an even 300 watts to overcome rolling resistance.
Aerodynamic Drag
Aerodynamic drag is governed by the drag equation:
$$F_{D}=\frac{1}{2}\rho v^{2}AC_{D}$$
Where \(F_{D}\) is drag force. \(\rho\) is air density. \(v\) is velocity. \(A\) is frontal area and \(C_{D}\) is drag coefficient. I need a final result of power to overcome aerodynamic drag and power is equal to force mutiplied by velocity. Power to overcome aerodynamic drag is:
$$P_{D}=\frac{1}{2}\rho v^{3}AC_{D}$$
\(P_{D}\) goes up as the cube of velocity, and given that we can only marginally change air density (hotter air and higher altitudes have lower density air), reducing \(A\) and \(C_{D}\) becomes very important. I’ll plug in some numbers to find out what kind of power is associated with what kinds of \(C_{D}\) values. Starting with:
Frontal Area
Aerovelo claims to have achieved a frontal area \(A\) of .325m\(^2\). To be conservative for this analysis i’ll use \(A=.35\)
Fluid Density
The fluid in this case is air, and I’ll use the air density on a standard day at the altitude where human powered vehicle records are tested. Battle Mountain, NV is at 4,600ft elevation (1402m). This corresponds to an air density of \(\rho =1.07 \frac{kg}{m^3}\)
Drag Coefficient
The \(C_{D}\) is difficult to compute without using computational fluid dynamics (CFD) simulations, and even with CFD, I am personally constrained by my shallow knowledge of the topic, but I’ll get to that eventually.
I’ll try some drag coefficients associated with a variety of shapes. Here is a table of drag coefficients from Wikipedia in fluids with Reynolds Number ~ \(10^4\).
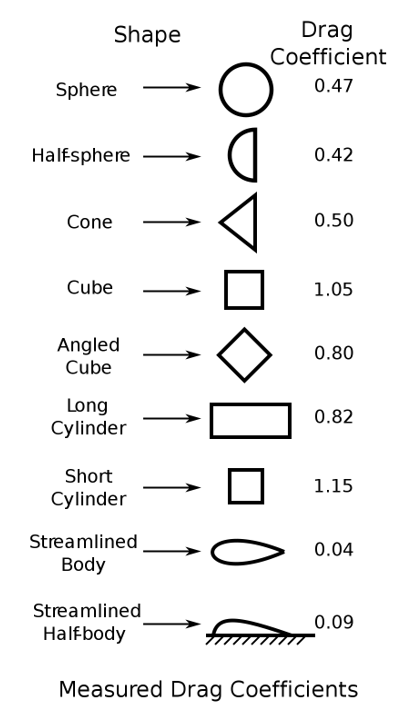
While \(10^4\) is an inappropriate Reynolds number for this application, the chart still shows the dramatic differences in drag coefficients for streamlined bodies.
I’ll start with these:
| Drag Coefficients to Test |
| .82 (long cylinder) |
| .47 (sphere) |
| .0383 (Aerovelo Eta) |
Velocity
Velocity is 100mph – or 44.704 meters per second in SI units.
Solving for Power to Overcome Aerodynamic Drag
$$P_{D}=\frac{1}{2}\rho v^{3}AC_{D}$$
| Frontal Area | Fluid Density | Velocity | Drag Coefficient | Power |
| .35 | 1.07 | 44.704 | .82 | 13,717 |
| .35 | 1.07 | 44.704 | .47 | 7,862 |
| .35 | 1.07 | 44.704 | .0383 | 640 |
The difference in power between a long cylinder and Aerovelo’s Eta is enormous. Drag coefficient matters a lot at these speeds. You can control Frontal Area \(A\) and Fluid Density \(\rho\) as well, but they have practical limitations.
Frontal area can be reduced down to the size of person cycling lying down. There must be enough room in the vehicle for their knees to move up and down, a drive-train, wheels, fairing, and any equipment needed.
Fluid density can only be reduced by testing on a hot day or at very high altitude. The test must be performed on the ground, and since the competition is at a fixed location, it is not practical to count on lower air density.
Drag Coefficient can be reduced by changing the vehicle shape, and based on the claims of the Aerovelo team, the Eta has achieved a very low drag coefficient at .0383. I’ll use .04 to be conservative when calculating a final power to overcome drag.
$$P_{D}=\frac{1}{2}\rho v^{3}AC_{D} = \frac{1}{2}(1.07)(44.704)^{3}(.35)(.04) = 670 watts$$
670 watts to overcome aerodynamic drag.
Final Power
Recall that total power is:
$$P_{total} = \frac{P_{R}+P_{D}}{\eta}$$
I have found here that it takes 670 watts to overcome aerodynamic drag, and 300 watts to overcome rolling resistance. I have not made any assumptions about drive-train efficiency. Through Wikipedia I found this book which claims 1-7% reduction in efficiency with a traditional gearing system. I’ll use 3%.
$$P_{total} = \frac{300+670}{.97} = 1000 watts$$
By chance, it comes out to 1,000 watts exactly. Which is within reach for a cyclist. However this is instantaneous power, or the power it takes to maintain 100 mph at any instant on flat ground with no wind. It does not consider the effort it takes to accelerate up to to 100 mph.
If 1,000 watts is achievable, why didn’t the Aerovelo reach 100 mph? It could be the acceleration effort that holds the rider back from going faster. The rider must output enough power to overcome the increasing rolling resistance and aerodynamic drag during the entire time accelerating.
Summary
It takes ~1000 watts on paper to maintain 100 mph in an incredible vehicle like the Aerovelo Eta.
Based on the very incremental improvement of the record thus far, it seems to be a substantial feat to reach 89 mph. Understanding the difficulty of accelerating to such high speeds will give a better insight into the challenge of reaching high speeds under human power, which I will look at in the next post.
I look forward to your next post.